L'expansion des probabilités

-Bernouilli et son théorème

En 1713, Jakob Bernoulli publie un autre traité sur les probabilités plus complet que celui de Huygens.
Il aborde le lien entre probabilités et fréquences en cas de tirages répétés (d’un jeu de pile ou face). Il énonce et démontre la loi faible des grands nombres pour ce jeu, appelé Théorème de Bernoulli :

Bernoulli, dans son traité, énonce aussi des éléments concernant les problèmes de dénombrement. Il poursuit les travaux des Chinois et des Indiens et ceux que Leibniz exprimait de façon beaucoup trop succincte.
Il rédige la théorie des permutations et des combinaisons et rédige la loi binomiale.

Une épreuve de Bernoulli conduit à la création d'un univers Ω = {S ; E}.
n épreuves de Bernoulli indépendantes conduisent à la création d'un univers Ωn constitué de n-uplets d'éléments de Ω, sur lequel peut se définir une probabilité produit. La probabilité de l'éventualité (S, S, ..., S, E, E, ..., E) avec k succès et n - k échecs a donc pour valeur .
Plus généralement, lors d’une expérience basée sur n essais et composée de k succès et de n-k échec, la probabilité est      quel que soit l'ordre d'apparition des S et des E.
 Il s’agit de dénombrer le nombre d’expériences comportant k succès et n-k échec. Il faut donc trouver le nombre de parties à k éléments dans un ensemble qui en compte n. Parmi les n places disponibles, on peut placer les k succès de  façon. = =
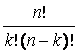
On obtient donc

-Formule générale de probabilités

3 ans plus tard, Abraham de Moivre énonce la formule générale de probabilité. L'apport de De Moivre est fondamental en probabilités notamment son ouvrage « doctrine of chance ». C’est dans cet ouvrage qu’il explique comment calculer la probabilité d'un événement aléatoire qui dépend de plusieurs autres événements : c'est la formule des probabilités composées.
De Moivre est aussi le premier à s'intéresser à la convergence des variables aléatoires, sous l'optique suivante : dans quelle mesure peut-on être sûr que lorsque l'on lance un grand nombre de fois un dé, la fréquence observée d'apparition du nombre "six" tend vers la probabilité théorique. De Moivre montre en particulier que la loi binomiale tend, en un certain sens, vers la loi normale (ou loi de Laplace-Gauss), la fameuse loi "à la courbe en cloche".

En 1812, Simon de Laplace publie « théorie analytique des probabilités ». Il y écrit une définition rendant concrète l’idée de probabilité.

A la même époque, le sens et la définition mathématique de probabilité font l’objet de nombreux débats.
Certains mathématiciens tels que D’Alembert se méfient de cette branche, ils  considèrent que ces méthodes comme beaucoup moins rigoureuses que celles de la géométrie. Pour eux, la science donne aux hommes la possibilité de connaître les Lois de l’Univers, rien ne peut être dû au hasard. Laplace répond que les phénomènes aléatoires n’ont d’aléatoires que le nom mais c’est à cause de leur complexité que nous ne pouvons les comprendre. Les probabilités peuvent être une aide pour en savoir davantage sur ces phénomènes.

Condorcet pense que les probabilités peuvent aussi s’appliquer à l’étude des phénomènes économiques et sociaux.

Quelques années plus tard, les probabilités servent désormais aux assurances qui sont en pleines expansion. Le métier d’actuaire apparaît. Métier qui utilise les mathématiques pour estimer par exemple, les pertes lors d’un accident ou la durée de vie. 

Les probabilités s’étendent ensuite à la médecine et à la biologie. Elles permettent aussi le développement de la mécanique statistique et de la théorie cinétique de la matière

En 1933, Andreï Nikolaïevitch Kolmogorov publie son Fondements de la théorie des probabilités dans lequel il met en place une axiomatique qui a été très largement acceptée par les mathématiciens

Retour au menu