

▪ Méthode de jeu
La roulette est un jeu très simple. Lorsque vous prenez part à une partie de roulette, vous devez d'abord acheter des jetons du croupier, d’une couleur particulière, que vous devrez encaisser à la fin du jeu. Il vous suffit ensuite de miser sur un ou plusieurs numéros. Le croupier tourne la roue dans un sens et lance une bille sur le contour de la roue dans le sens opposé. Une fois que la vitesse de la bille commence à ralentir, on ne peut plus miser. Le joueur a alors le droit de miser jusqu’à ce que le croupier annonce « rien ne va plus ». Toute mise suivant cette annonce est appelée « prise de pari retardée », et est considérée comme tricherie, car le joueur mise après avoir connu les résultats du tour.
Une fois que le résultat du tour est déterminé, le croupier place un marqueur sur le numéro gagnant. S’il y a des mises sur ce numéro, le croupier place le marqueur au dessus des jetons. Toutes les mises perdantes sont ensuite retirées de la table, avant que les mises gagnantes ne soient payées. La mise suivante doit être placée après que le croupier ait payé toutes les mises gagnantes.
▪Probabilités de gains à la roulette
Si l'on mise sur un seul numéro à la roulette, la probabilité de gain est de
P = (N/T) X 100
P = (1/37) X 100
P = 2,7%
Avec N = nombre de numéros concernés
P = probabilité de gain
T = total des numéros
Si l'on mise sur une "chance simple", c'est-à-dire sur le noir ou sur le rouge, la probabilité est de
E = (N/total) X 100
E = (18/37) X 100
E = 48,65 %
Le numéro restant étant le 0.
Voici un tableau récapitulatif des probabilités selon les nombres joués.
Nom de la chance jouée |
Nombre de numéros joués |
Probabilité de sortie(%) |
Numéro plein |
1 |
P = (1,0/37) X 100 |
Cheval |
2 |
P = (2,0/37) X 100 |
Transversale |
3 |
P = (3/37) X 100 |
Carré |
4 |
P = (4/37) X 100 |
Sizain |
6 |
P = (6/376) X 100 |
Douzaine ou colonne |
12 |
P = (12/37) X 100 |
Chance simple |
18 |
P = (18/37) X 100 |
Manque ou passe(18) + 1 |
24 |
P = (24/37) X 100 |
2 douzaine +1 sizain |
30 |
P = (30/37) X 100 |
On remarque donc que plus le nombre de numéros misés est grand, plus la probabilité de gains est importante. Cependant, il faut prendre en compte le fait que miser un numéro plein rapporte bien plus que de miser sur un sizain :
▪ Mises gagnées à la roulette selon le nombre de numéros joués.
Si le joueur mise sur un numéro plein, il gagne 35 fois sa mise.
Si le joueur mise sur un cheval il gagne 17 fois sa mise.
Si le joueur mise sur une transversale, il gagne 11 fois sa mise.
Si le joueur mise sur un carré, il gagne 8 fois sa mise.
Si le joueur mise sur un sizain, il gagne 5 fois sa mise.
Si un joueur mise sur une une douzaine, il gagne 2 fois sa mise.
Si le joueur mise sur une chance simple, il gagne 1 fois sa mise.
▪Roulette et espérance mathématique de gain
Comme nous l'avons vu précédemment, la première question à se poser lorsque
l'on participe à un jeu de hasard est : quelle est l'espérance mathématique de gain?
Pour cela, repartons d'un exemple très simple :
Un joueur A mise un euro sur un seul numéro, par exemple, sur le 12.
▪Quelques rappels sur l'espérance mathématique de gain
Si, pour cette mise, l'espérance mathématique de gain vaut 1, le jeu est équitable, si elle est plus grande que 1, le joueur est avantagé, si elle est inférieure à 1, c'est le casino qui est avantagé.
Si le joueur A gagne, c'est à dire si la bille tombe sur le 12, le joueur remporte 35 fois sa mise, soit 35 euros, plus sa mise, ce qui fait 36 euros. Cependant le joueur A a une 1 chance sur 37 de gagner.
Pour ce tour, l'espérance mathématique est de 36X 1/37 = 36/37 euros.
L'écart à 1, qui ici est de 1/37, correspond à ce qu'on appelle l'impôt du jeu, ou la cagnotte du casino. Ici, la cagnotte du casino est de 1/37 X 100 = 2,70 % de la mise.
▪L'impôt du jeu varie-t-il selon la chance multiple jouée ? L'avantage
du casino reste-t-il donc le même?
Pour cela, étudions la cagnotte du casino selon différentes chances multiples jouées, c'est-à-dire selon différents nombres de numéros joués.
1 – Le carré
Lorsqu'un joueur mise un euro sur un carré, c'est-à-dire sur 4 numéros, il remporte 8 fois sa mise + son euro de départ misé, soit 9 euros, d'après le tableau précédent, sa probabilité de tomber sur un numéro misé étant de 4/37.
Son espérance mathématique est donc de 9 X 4/37 = 36/37, soit exactement la même que pour un numéro plein.
L'avantage du casino est donc toujours de 2,70 % de la mise.
2- Le cheval
Lorsqu'un joueur mise un euro sur un cheval, c'est à dire sur 2 numéros, il remporte 17 fois sa mise + son euro de départ misé, soit 18 euros, d'après le tableau précédent, sa probabilité de tomber sur un numéro mise étant de 2/37.
Son espérance mathématique est donc de 2 X 18/37 = 36/37, soit toujours la même que pour un numéro plein.
L'avantage du casino est encore de 2,70% de la mise.
3 – La chance simple
Pour la chance simple, le calcul est légèrement différent.
En effet, lorsque le zéro sort, les chances simples sont mises « en prison », c'est-à-dire que les mises sont laissées sur le tapis de jeu et reportées à la bille suivante.
Entre temps, le joueur peut, s'il veut, modifier son jeu, c'est-à-dire changer de numéros.
A la bille suivante, si la chance simple gagne, le joueur peut reprendre sa mise, mais il n'est pas payé. Si le joueur perd, c'est le casino qui ramasse la mise. Si le zéro sort deux fois de suite, les mises sont emprisonnées pour deux billes et ne sont récupérables que si l'on gagne deux fois de suite.
Imaginons que le zéro ne sort qu'une seule fois, et que le joueur ait misé 1 euro. En effet, il est rare que le zéro sorte deux fois de suite. La probabilité pour qu'il sorte deux fois de suite est de 1/(37X37), soit 1/1369.
Au premier coup, le joueur a 18 chances sur 37 de gagner, et si le zéro sort (il y a une chance sur 37 que cela se produise), le joueur a une chance sur deux de récupérer sa mise.
D'après le tableau précédent et la définition de l'espérance mathématique, l'espérance mathématique est de :
E = 18/37 X 2 + 1 X 1/37 X ½
On obtient
E = 73/74
L'écart à 1 est de 1/74, donc l'avantage du casino est de 1/74 X 100 = 1,35%
L'impôt du jeu est 1,35%, soit deux fois moins que sur les chances multiples. On ne peut cependant pas conclure qu'il est plus intéressant de jouer sur les chances simples, mais on peut affirmer que l'avantage du casino est plus faible. L'intérêt du casino est donc que les joueurs jouent sur des chances multiples, et non sur des chances simples.
▪Évolution des chances de gain selon le nombre de parties
Si un joueur A joue un coup sur un numéro, il a 1 chance sur 37 de gagner, donc
36 chances/37 de ne pas gagner.
Sa probabilité de ne pas gagner est donc de 0,97.
Si ce même joueur joue deux coups, il a toujours 36 chances sur 37 de ne pas gagner au premier coup et donc également 36 chances sur 37 de ne pas gagner au second coup. Sa probabilité de ne pas gagner en deux coups est donc de
(36/37)² = 0,94
En deux coups, la probabilité de ne pas gagner est donc plus faible.
Plus généralement, si l'on appelle n le nombre de parties, on a (36/37)n chances de ne pas gagner, on a donc 1 – (36/37)n de chances de gagner au moins une fois.
Pour mieux se représenter ce principe, traçons le graphique représentant la probabilité en fonction du nombre de coups.

D'après le graphique, on remarque que pour avoir une chance sur deux de gagner
au moins une fois sur un numéro, soit 0,5 sur ce graphique, il faut jouer environ
25 parties.
Si l'on veut être certain (ou presque) de gagner au moins une fois sur un numéro, il faut jouer environ 175 coups.
Or, si l'on réfléchit, si l'on mise un euro sur un seul numéro, on risque 170 euros, pour en gagner seulement 36 ! (35 fois la mise + l'euro misé).
Si le joueur ne veut pas jouer autant de parties, il peut jouer d'autres chances multiples. On remarque par exemple que si l'on joue un sizain, il faut environ 4 coups pour avoir une chance sur deux de gagner et 25 coups en moyenne pour avoir une quasi-certitude de gagner.
Le nombre de parties est beaucoup plus faible, cependant les gains aussi!
On remarque de nouveau le sérieux avantage du casino.
Ces calculs nous donnent donc la probabilité de gagner au moins une fois selon le nombre de parties.
▪Comment connaître la probabilité de gagner exactement k fois en n parties ?
Pour simplifier les calculs, on suppose que le joueur joue toujours sur un numéro plein (1 seul numéro).
Si p est la probabilité de gagner, alors 1-p est la probabilité de perdre. Pour simplifier les calculs, notons q la probabilité de perdre, q est donc égal à 1-p.
On souhaite connaître la probabilité de gagner 1 fois en n parties.
Ainsi, il faut donc gagner 1 fois (probabilité p) et donc perdre n-1 fois : probabilité qn-1.
En effet, en un certain nombre de parties, pour gagner 1 seule fois, il suffit de perdre toutes les autres et donc de perdre n, le nombre de parties, moins 1, la partie gagnée.
La probabilité de gagner 1 fois en n parties est donc de
![]() .
.
Cependant, le gain peut se produire au premier coup, ou au deuxième, ou
troisième ou au nième. La probabilité est donc
![]()
De la même façon, si l'on veut gagner 2 fois en n parties, il faut gagner 2 fois (probabilité p2 ) et donc perdre n-2 fois, la probabilité est alors de
![]()
Cependant, il y a plusieurs façons de choisir les deux coups gagnants parmi les n coups joués. Tout comme pour 1 seul gain, le gain peut se produire au premier, second, nième coup, il y a en effet n(n-1)/2 façons de le réaliser, n-1 étant la perte, n le nombre de coups et 2 le nombre de gains.
On note ![]()
La probabilité de 2 gains en n parties est donc de ![]()
Si l'on généralise cette probabilité à k gains pour un nombre n de coups, on
obtient alors : P k = ![]()
Mise en pratique
Calculons la probabilité de gagner 1 fois exactement en 88
coups :
Rappelons que ici, dans le cadre du jeu de roulette, p= 1/37
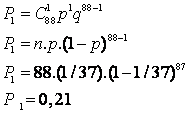
La probabilité est donc de 0,21.
Essayons maintenant de calculer la probabilité de gagner 4 fois exactement en 150 coups :
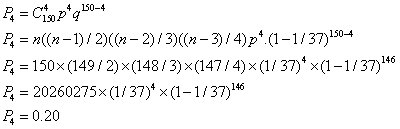
La probabilité est donc de 0,20.
Nous pouvons ainsi tracer la courbe représentant
probabilité de gagner exactement 1,2,3 ou 4 fois sur 1 numéro plein :

En traçant cette courbe, on remarque que pour chaque gain, la courbe augmente et atteint un maximum, puis redescend. En effet, plus le nombre de parties augmente, puis la probabilité de gagner plusieurs fois augmente, ensuite celle-ci diminue car la probabilité de ne gagner qu'une seule fois en de très nombreux coups diminue.
▪Probabilité de perdre
Grâce à nos précédents calculs, nous allons maintenant nous intéresser au joueur trop sûr de lui, qui ne cesse de jouer sur des chances simples, sans perdre une seule partie, et en misant toujours la même chose.
Quelle est sa probabilité de perdre au bout de n parties s’il joue toujours sur des chances simples ?
Remarque : afin de simplifier le calcul, nous ne tiendrons pas compte de l’exception du zéro en imaginant que, lorsqu’il sort, le joueur perd sur ses chances simples.
Puisqu ’il joue sur 18 numéros, sa probabilité à la roulette est donc 18/67. Pour que le joueur soit perdant au bout de n coups, il suffit qu’il n’ait pas gagné plus de n-1 fois, soit qu’il ait gagné une fois, deux fois, trois fois… le tout jusqu’à n-1 fois.
La probabilité pour qu’il n’est pas gagné plus de n-1 fois est donc la somme de
toutes les probabilités pour qu’il ait gagné une fois, deux fois… jusque n-1 fois.
Nous pouvons donc en déduire la formule suivante.
P = ![]()
▪ Roulette et martingales
Une martingale est une technique mathématique qui permettrait d’augmenter les chances de gain aux jeux de hasard.
1 – La martingale de d’Alembert
Martingale de d’Alembert (ou montante d’Alembert) : la mise initiale est de K francs ; ensuite, à chaque fois que vous gagnez, vous diminuez votre mise de K francs (parce que vous pensez que la chance vient de vous être favorable, et qu’elle risque de l’être moins le coup suivant) et à chaque fois que vous perdez vous l’augmentez de K francs (car vous croyez maintenant que la chance peut vous servir)
Ainsi, prenons un exemple. Misons 5euros sur une chance simple, par exemple sur le rouge. Si la bille tombe sur le rouge, on gagne une fois notre mise, soit 5 euros, ce qui fait 10 euros avec note mise initiale. Le coup suivant, puisque l’on a gagné, on mise donc encore 5 euros.
Si maintenant, la bille tombe sur le noir, on perd donc 5 euros. Il faut donc miser pour la fois suivante la mise précédente ainsi que la mise de départ de 5 euros.
Il suffit donc simplement, selon d’Alembert, d’enlever la mise initiale lorsque l’on gagne, et d’ajouter cette même mise lorsque l’on perd.
Regroupons cet exemple dans un tableau :
Couleur |
Résultat |
Mise |
Résultat (mise initiale + gain) |
Cumul des gains/pertes |
Rouge |
Noir |
5 |
-5 |
-5 |
Rouge |
Noir |
10 |
-10 |
-15 |
Rouge |
Noir |
15 |
-15 |
-30 |
Rouge |
Rouge |
20 |
40 |
-10 |
Rouge |
Rouge |
15 |
30 |
5 |
Rouge |
Rouge |
10 |
20 |
15 |
Rouge |
Noir |
5 |
-5 |
10 |
rouge |
rouge |
10 |
20 |
15 |
On remarque que pour une mise de 5 euros, pour un même nombre de coups gagnants ou perdants, le bénéfice du joueur est de 15 euros.
Avec cette méthode, lorsqu’il y a équilibre entre les coups gagnants et perdants, on fait donc un bénéfice. La limite de cette méthode est atteinte dans le sens où le nombre de coups perdants est supérieur au nombre de coups gagnants.
2 – la martingale géométrique
Cette martingale, également appelée martingale classique, est très connue. Elle consiste en effet à miser K francs au départ. Si le joueur perd, il double sa mise, et continue toujours à al doubler jusqu’à ce qu’il arrive à gagner.
Ainsi, le joueur perd K + 2K + 4K + 6K…….+2n+1K et l’on gagne donc 2n+1 K. Il a donc en tout gagné K euros.
Prenons un simple exemple : on mise 1 euro. On perd, on mise alors 2 euros, on perd encore, on mise 4 euros, puis l’on gagne.
Au total, le joueur a donc perdu 3 euros et gagné 4 euros, il a donc reçu 1 euro., soit sa mise de départ.
Cette méthode semble être efficace et le joueur pourrait alors, s’il n’arrête pas de doubler sa mise, gagner beaucoup d’argent.
Cependant, lorsque le joueur n’a plus d’argent, il ne peut plus miser. De plus, le casino fixe un nombre limite de mises, le joueur ne peut donc pas miser autant qu’il le souhaite…
Ainsi, cette martingale peut profiter aux joueur qui peuvent miser gros :
si un joueur mise deux euros, et qu'au bout de 7 coups, il n'a toujours pas gagné, il a donc perdu 2 + 4 + 8 + 16 + 32 + 64 + 128 = 254 euros
Si, au bout du 8ème coup, le joueur gagne, il empoche alors 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 2 (mise initiale) = 512 euros, alors qu'il aura déboursé 2+4+8+16+32+64+128+156 = 510 euros, il ne gagne pour finir que 2 euros, le joueur est donc gagnant mais il lui a fallu tout de même débourser 500 euros.
Cette méthode s'avère donc dangereuse dans le sens où, sil le joueur souhaite appliquer cette méthode avec seulement 200 euros, il aurait du s'arrêter au 7 ème coup puisqu'il n'a pas assez d'argent pour miser deux fois la mise précédente, il aurait alors perdu 2 + 4 + 8 + 16 + 32 + 64 = 126 euros.
Imaginons également les dégâts que cette méthode peut engendrer à cause du zéro, de la mise « prisonnière ».
En effet, alors que si le joueur n'a toujours pas gagné, il continue de doubler sa mise, si la bille tombe sur le zéro, celle-ci reste « en prison ». Or, la martingale géométrique consiste à ne s'arrêter de jouer que lorsqu'on a gagné. Cependant, plus l'on joue, plus la probabilité de tomber sur un zéro augmente, et donc plus on risque de perdre..
Comme pour chaque martingale, la chance ne joue pas un rôle négligeable dans les jeux de hasard.