

Stratégies au Blackjack
Les règles du jeu de black jack ont été définies pour que le casino ait un faible avantage.
Selon les règles et le nombre de jeux utilisés, cet avantage varie.
Soit P(x) la probabilité de gain du joueur, alors P(1-x) le probabilité de perte du joueur, donc P(1-x) la probabilité de gain du casino.
Avantage supérieur au casino :
Si le croupier et le joueur sautent tous les deux, le croupier gagne.
En jouant le premier, le joueur qui passe au-dessus de 21 perd sa mise. L'argent n'est pas rendu si le donneur saute lui-aussi. C'est le seul déséquilibre qu'il y a dans le jeu, en faveur du casino.
En considérant que même avec une stratégie de base bien rodée, le joueur saute dans environ 16% des cas, c'est un avantage important.
Comment augmenter la probabilité de gain du joueur ?
La première manière de diminuer les probabilités en faveur du joueur est d’utiliser la stratégie de base. La stratégie de base du black jack varie selon les règles et le nombre de jeux de cartes compris dans le sabot. Il s’agit de suivre le tableau des stratégies de base. Un joueur qui joue sans stratégie peut s’attendre à des probabilités entre 3 et 5% en faveur de la maison en fonction des règles appliquées.
En utilisant la stratégie de base il possible de baisser cet avantage de la maison à moins de 1% .Voici un exemple de tableau de la stratégie de base applicable en France
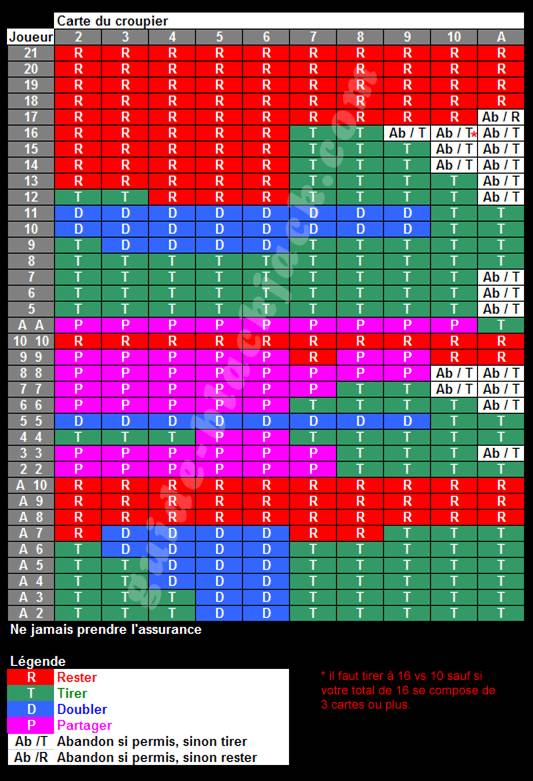
La stratégie de base est aussi la base du comptage de cartes. La stratégie de base peut évoluer en fonction du comptage des cartes.
Le principe du comptage des cartes consiste à attribuer des valeurs (+1, 0 ou -1) à chaque carte distribuée aux joueurs et au donneur, et à additionner les valeurs pour savoir si les cartes restantes dans le sabot sont à l’avantage du joueur ou non. C’est un système de comptage équilibré
Le système High-Low est un exemple de comptage de cartes équilibré. Il y’a autant de +1 que de -1 dans le jeu, donc un comptage des 52 cartes est à 0 au début et donne 0 à la fin.
Les As ainsi que les bûches (cartes équivalant à 10 au blackjack, soit la dame le roi et le valet) prennent la valeur -1 dans ce système, car le retrait de ces cartes du sabot désavantage le joueur, si elles ne sont pas dans le sabot le croupier a moins de chance de dépasser 21. En effet si on venait à enlever tous les as du sabot, le casino serait avantagé.
Les cartes 7, 8, 9 valent 0.
Les cartes 2, 3, 4, 5 et 6 comptent chacune +1, car le retrait de ces cartes du sabot avantage le joueur.
Plus le true count est élevé, plus nombre de bûches présentes dans le sabot est élevé, plus la partie tourne à l’avantage du joueur : il augmente sa mise. De même, lorsque le compte est faible, il y a moins d’As dans le sabot donc moins de chances pour le deal de faire un bust, ce qui désavantage le joueur, le compteur fait alors des mises minimales.
Modification de la stratégie de base par rapport au compte :
Les compteurs de carte prennent une assurance uniquement lorsque : TC>3 ou TC=3 avec TC le vrai compte.
Cette technique présente une difficulté pour le joueur qui se doit de calculer mentalement le nombre de restant tout au long du jeu.
La première colonne de ce tableau indique les chances du croupier de sauter (dépasser 21), selon sa première carte. On remarque que la plus grande chance de faire un bust est lorsque la première carte du croupier est un 5.
La troisième colonne indique l’avantage du joueur utilisant la stratégie de base du black jack, selon la première carte du croupier. Le joueur a le plus de chances de gagner lorsque le croupier a un 5 en carte découverte. L’avantage est négatif pour le joueur lorsque le croupier a un 9 ou plus.
Carte ouverte du croupier |
Probabilité de sauter du croupier |
Avantage du joueur avec la stratégie de base |
2 |
35.30% |
9.8% |
3 |
37.56% |
13.4% |
4 |
40.28% |
18.0% |
5 |
42.89% |
23.2% |
6 |
42.08% |
23.9% |
7 |
25.99% |
14.3% |
8 |
23.86% |
5.4% |
9 |
23.34% |
-4.3% |
10,V,D,R |
21.43% |
-16.9% |
A |
11.65% |
-36.0% |
Pour ce tableau, il s’agit d’analyses combinatoires et de simulations, ces calculs font appel à de nombreux cas particuliers. Cependant nous allons essayer de retrouver la probabilité de sauter du dealer, qui est de 21,43% lorsque le croupier a une bûche (carte à valeur de 10 comme première main). On pose D(x)la deuxième carte tirée du croupier, et T(x)la valeur totale de sa main. Dans cette situation le croupier s’arrête de tirer des cartes dès que T(x)>17 ou T(x)=17, il s’agit de la règle Hit 17, alors:
- la probabilité de s'arrêter après le tirage de la carte suivante est 8/13. Il y a 10 dans sa main donc il s’agit de la probabilité que sa main vaut ou dépasse 17, le 8 correspond aux cartes 7, 8, 9, 10, V, D, R et As, elles vérifient : 10+ D(x)=17 ou 10+D(x)>17. Le 13 correspond aux différentes possibilités de types de cartes tirées soient les cartes allant de 2 à l’As.
Si T(x)<17, c'est qu'il a tiré une carte < 7, donc :
-> S’il a tiré un 6, T(x)=16 et il tire encore une carte. La probabilité d'arrêter avant d'exploser, de buster est 4/13. Le 4 correspond aux cartes dont la valeur vérifie 16+ D(x)<21, soit les types de cartes dont la valeur est inférieure à 6. Donc la probabilité qu'il ait tiré un 6 puis une carte et s'arrête est 1/13 * 9/13. Le 1/13 correspond à la probabilité de tirer une carte de valeur 6 sur les 13 sortes de cartes possibles, le 9/13 correspond quant à lui à la probabilité que D(x’), où D(x’) est la troisième carte tirée par le croupier et qui vérifie 16+D(x’)>21 soit D(x’)>5. Cette probabilité reste approximative car nous n’avons pas pris en compte la non indépendance des valeurs des cartes tirées, c'est-à-dire que lorsqu’il tire un 6 par exemple à un moment donné, la probabilité de tirer un 6 après le retrait de ce 6 du sabot est plus faible que elle qu'il tire une autre carte puisque le nombre de 6 restant dans le paquet de cartes est moindre. Il s’agit donc bien d’une première approximation.
->S'il a tiré un 5, T(x)=15 et il tire encore une carte. Par un même raisonnement, la probabilité qu'il ait tiré un 5 puis une carte et s'arrête est 1/13 * 8/13 approximativement. Le 8/13 correspond aux sortes de cartes qui vérifient 15+D(x’)>21, c'est-à-dire la probabilité que: D(x’)>7.
->S'il a tiré un 4, T(x)=14 et il tire encore une carte. La probabilité qu'il ait tiré un 4 puis une carte et s'arrête est 1/13 * 7/13. 7 /13 est la probabilité que D(x’) vérifie 14+D(x’)>21 soit D(x’)>8. La probabilité que D(x)=4 et que D(x’)=2 par exemple, puis que le croupier tire encore une carte puis s'arrête est 1/13 * 1/13 * 5/13. 5/13 correspond à D(x ″) où D(x″) est la valeur de la quatrième carte tirée et qui vérifie :
10+4+2+ D(x ″)>21.
->Si D(x)=3, T(x)= 13 et il tire encore une carte. La probabilité que D(x)= 3 et que D(x’)>8 est 1/13 * 6/13 . La probabilité qu'il ait tiré un 3 puis un 2 puis une autre carte puis s'arrête est 1/13 * 1/13 * 4/13. La probabilité qu'il ait tiré un ait tiré un 3 puis un 3 puis une autre carte puis s'arrête est 1/13 * 1/13 * 4/13.
Ainsi de suite pour toutes les possibilités. Il s’agit désormais de faire la somme :
8/13 + 1/13 * 9/13 + 1/13 * 8/13 + 1/13 * 7/13 + 1/13 * 1/13 *6/13 + 1/13 * 5/13 + 1/13 *1/13 * 4/13 + 1/13 * 1/13 * 4/13 1/13 * 1/13 * 4/13 + 1/13 * 1/13 * 4/13 + Tous les autres termes car il y en a de plus en plus, qui sont de plus en plus petits...
Cela nous donne la probabilité que le croupier s'arrête avec une somme inférieure ou égale à 21, donc n'explose pas. Donc la probabilité qu'il brûle est 1 – la somme précédente.
Pour approximation numérique, la somme des termes ci dessus fait 0,7988 donc 1- 0,7988 =0.2011, ce qui n'est pas tellement éloigné de la valeur mentionnée de 21.43%. Maintenant il y existe sûrement des techniques plus intelligentes et plus automatisées pour calculer ces probabilités…
Application, mise en pratique par l’équipe du M.I .T :
Afin de gagner au casino sans se rendre suspect, être en équipe est plus efficace. Il y a alors division du travail, en effet il est aisé de détecter un compteur de cartes isolé, qui augmente et baisse ses mises selon le décompte en cours, alors qu’il est plus difficile de détecter une équipe de qui a l’air de n’avoir aucune relation. L’utilisation du comptage de cartes est légale en France néanmoins le joueur qui gagne régulièrement peut être se voir refuser l’entrée des casinos.
Il y avait trois rôles principaux dans cette équipe : le Détecteur, le Gorille et le Gros Joueur. Le Détecteur était un compteur de carte, qui misait toujours le minimum. Lorsqu’ un décompte devenait positif, c’est à dire avantageux pour les joueurs car la somme de cartes fortes restantes dans le sabot est importante, le Détecteur le signale au Gorille ou au Gros Joueur. Le Gorille ne comptait pas: il jouait simplement de grosses mises quand on leur disait de le faire. Le Gros Joueur est un gorille avancé, qui comptait avec le Détecteur lorsqu’il était appelé à une table et il réussissait à déjouer l’attention du casino en variant ses mises. Dans chaque cas, l’important était de pouvoir jouer de grosses mains (1000 $ ou plus) sans se comporter comme un compteur de cartes. Et comme le Gorille et le Gros Joueur ne venaient sur la table que lorsque le compte était très élevé, ils ne pouvaient être accusés de compter les cartes.
Les surveillants du casino s’y sont fait prendre, c’était alors une des toute premières applications de la stratégie d’Edward Thorp en équipe. Pour communiquer entre eux ils utilisent alors des signes. Ainsi, le Détecteur croisait les bras pour signaler que la table était chaude, le Gros Joueur venant alors s’y asseoir jusqu’à ce que le sabot soit épuisé ou redevienne froid. Lorsque le sabot devient froid, le détecteur passe sa main sur le front et le gros joueur passe à une autre table. Le décompte était indiqué en utilisant des mots codés:
+1 = Arbre
+2 = Changer
+3 = Tabouret
+4 = Voiture
+5 = Gant
+6 = Pistolet
+7 = Craps
+8 = Billard
+9 = Chat
+10 = Bowling
+11 = Football
+12 = Œuf
+13 = Sorcière
+14 = Anneau
+15 = Paye
+16 = Sucré
+17 = Magazine
+18 = Isoloir
Le black jack donne statistiquement un avantage faible à la maison par rapport aux autres jeux de casino. En plus de la stratégie de base qui indique quand tirer, rester, doubler, abandonner, et partager, les joueurs peuvent utiliser le comptage de cartes pour améliorer leurs probabilités.